Fibonacci Sequence With Swift 4.0

One of the firsts examples is the Fibonacci Sequence, although It’s a common programming problem, also It’s a curious problem for be solve with swift.

This is a sequence of numbers, which start in the third element as the sum of the previous two numbers. The next number is the sum of the previous two numbers too.

0, 1, (0+1), (1 + (0+1))

0, 1, 1, 2, 3, 5, 8, 13

First Attempt

One of the common solutions for this problem is a recursive solution.

This solution implement a recursive solution, if you want to know numbers less than 2, you will get the same number, but if you want to know other number more than 2, you have to start a recursive code. This is a very common solution, for example if you want to know the Fibonacci sequence for the number 4, you will call the function 9 times. Our tool for swift It’s going to help us to see this.

Using Memoization

“Memoization is a technique in which we store the results of computational tasks when they are completed”

KOPEC, “Classic Computer Science Problems in Swift: Essential techniques for practicing programmers MEAP V04.”, Manning, 2017.

For this second solution we are using a Dictionary for save the firsts elements.

Using the number 4, if we want to know the 4th element in the sequence we only have to call the function only 3 times, because you are saving every element in the dictionary.

Using swift for solve the problem

We have other option for find other solution.

For example in Swift you can write this

/Pattern Matching/

let triple = (1, 2, 3)

let (x, y, z) = triple

This solution is going to implement pattern matching. We have only two variables: last and next. They must be initialized with 0 and 1. So, the next step is create a loop with n times for iterate a tuple pattern matching.

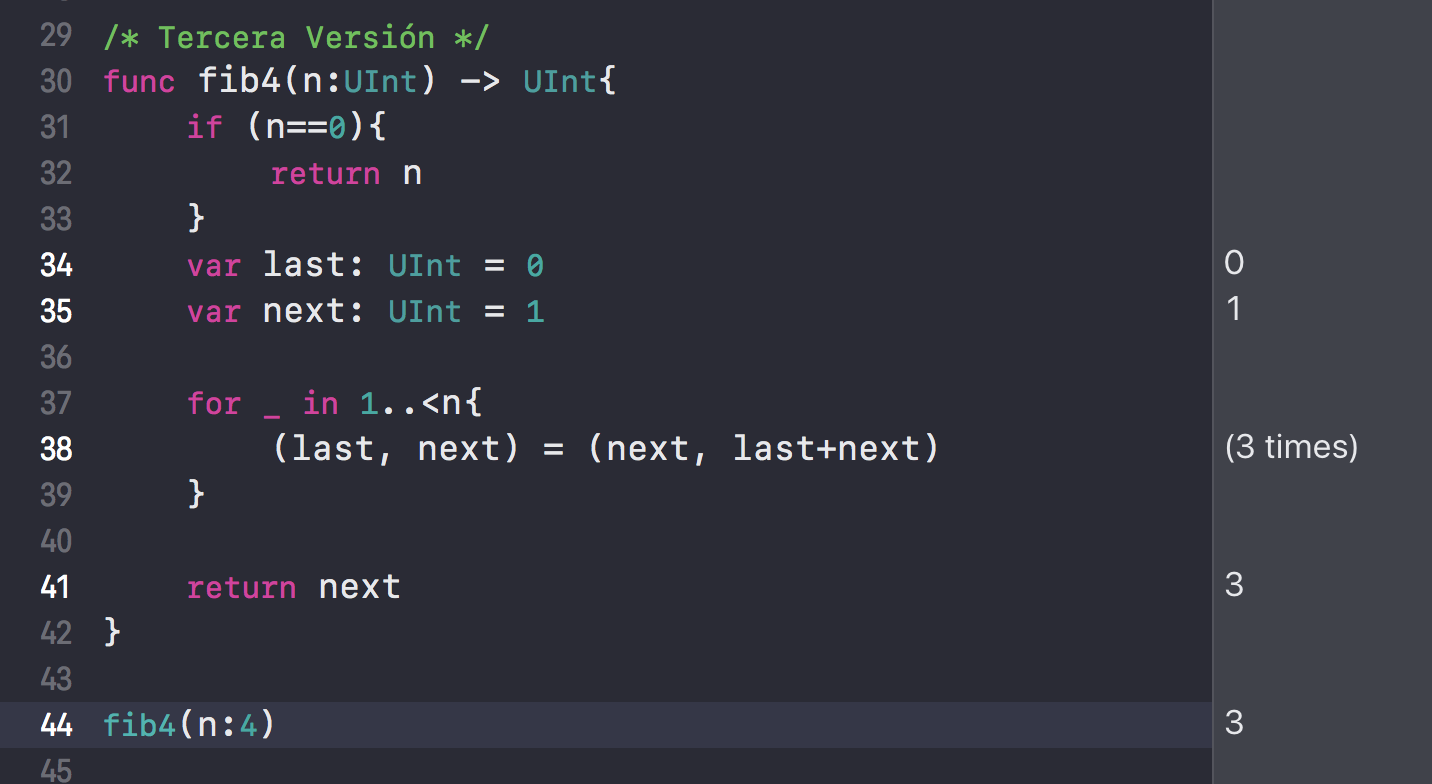
We are using pattern matching, and we aren’t using recursive anymore. What many times are we call the same function? Instead of this, we are call a loop.

Of course swift language have good tools for find new and simple solutions.

This is my first review of a part of the book Classic Computer Science Problems in Swift.

Thanks for reading!